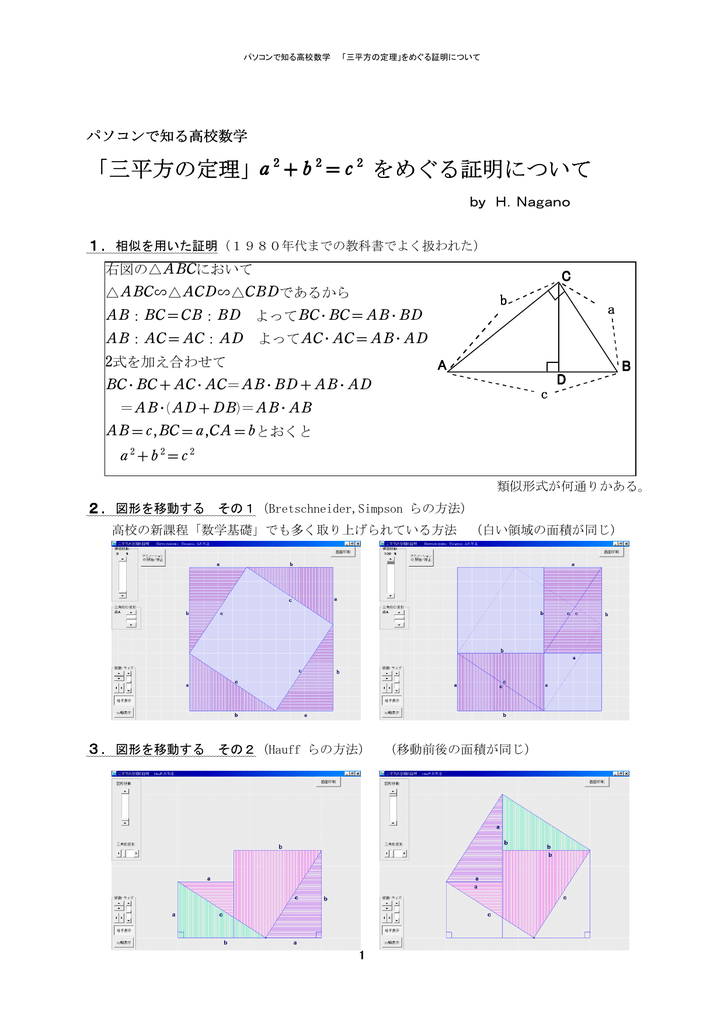
三平方の定理 方程式を利用する発展問題を解説 数スタ
中学数学正八角形の面積を三平方の定理で求める方法を解説! 三平方の定理 三平方の定理方程式を利用する発展問題を解説! それで、三平方の定理を使えば、 2× 2 =√3×√3+ 1 × 1 になることは納得できます。 そのため、次の内容は正しいことになります。 3 つの辺が√3と 2 と 1 の三角形は直角三角形になり、内側の角度は 90 度、 60 度、 30 度になる このことは三平方の定理から導くことができますが、では 3 つの辺のうち、「 1 」の長さが 2 倍になって「 2 」に変わったら、この関係はどうなるのでしょ
数学 三平方の定理 難問
数学 三平方の定理 難問- 中学校の数学で習う「三平方の定理(ピタゴラスの定理)」は ゲーム開発の中でも使われまくっている。 この理屈がなければあちこちが破綻するほどなので 先日紹介した三角関数以上に重要なものだと思っている。 三平方の定理とは そもそも三平方の定理とは 直角三角形における3つの辺数学円周角の定理 数学確率 数学乗法の公式 数学因数分解 数学素数 数学素因数分解 数学2次方程式 数学三平方の定理 数学2次関数 数学円周 数学平方根 数学相似図形 英語be動詞 英語疑問文・命令文

ある三平方の定理の証明方法 中学校程度の数学で理解しよう 身勝手な主張
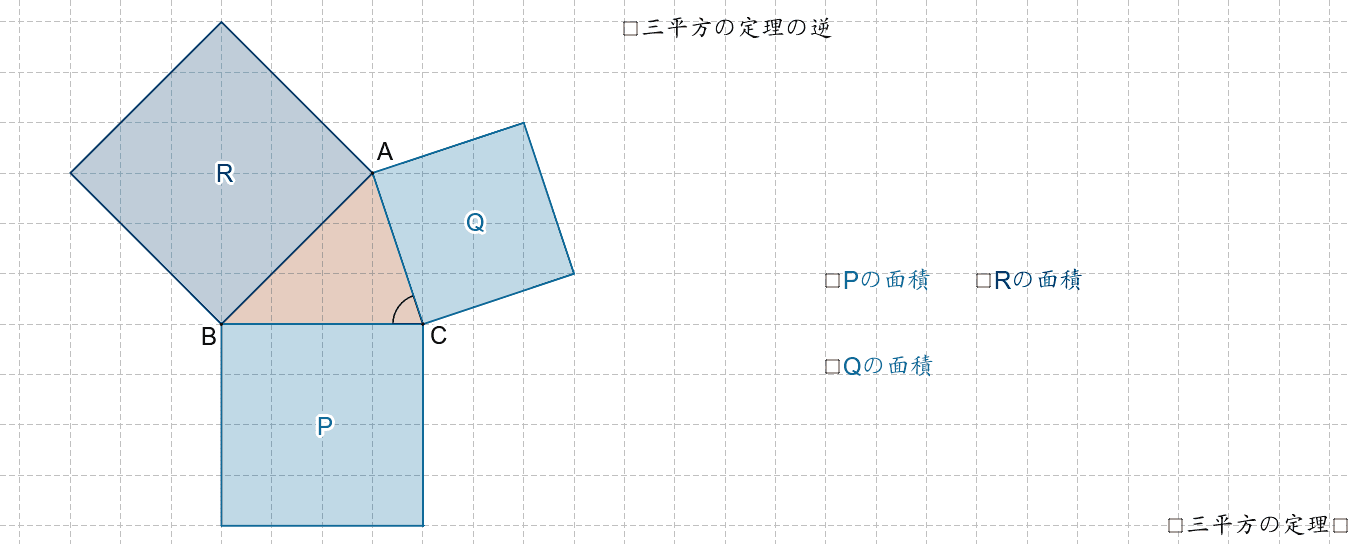
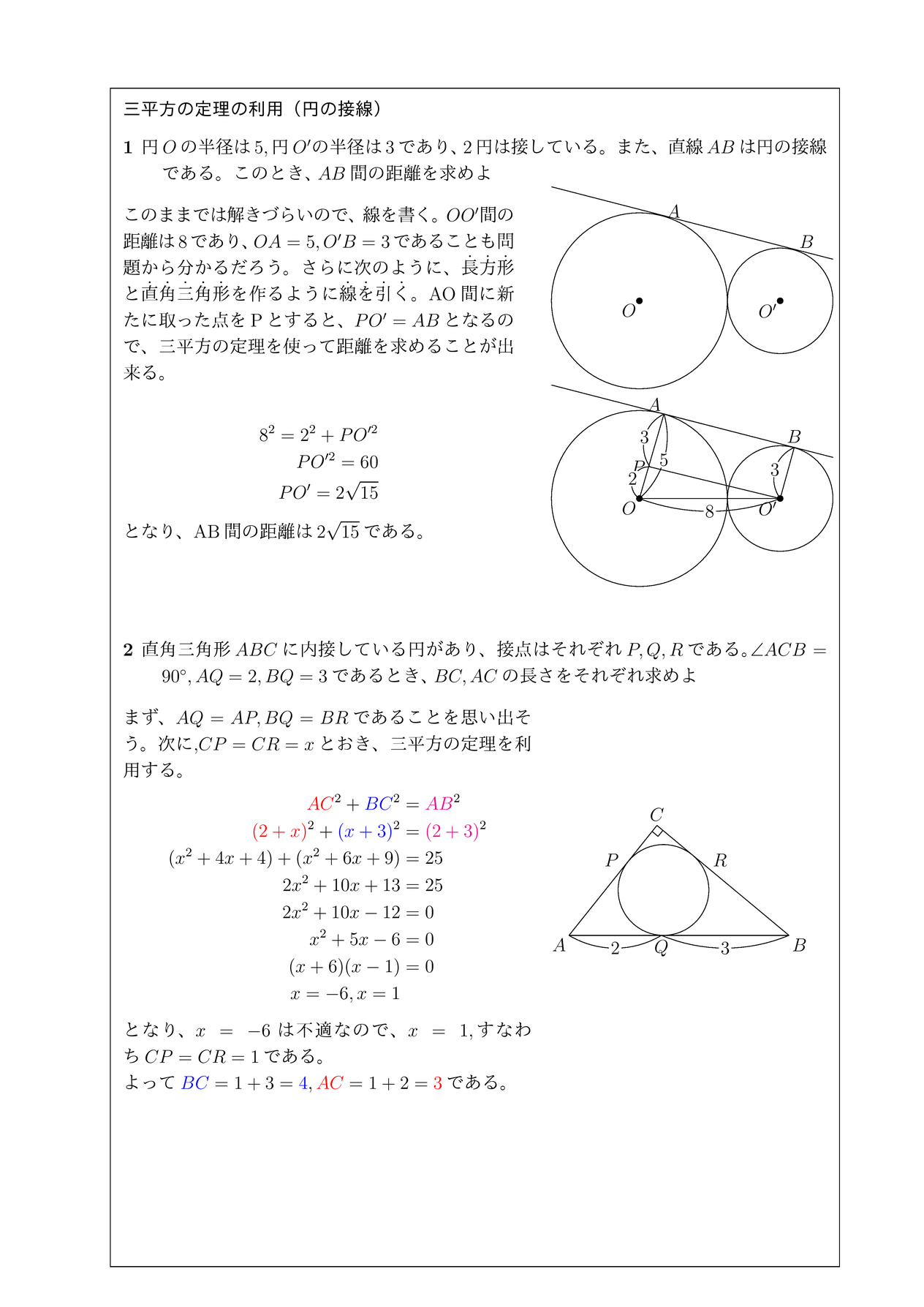
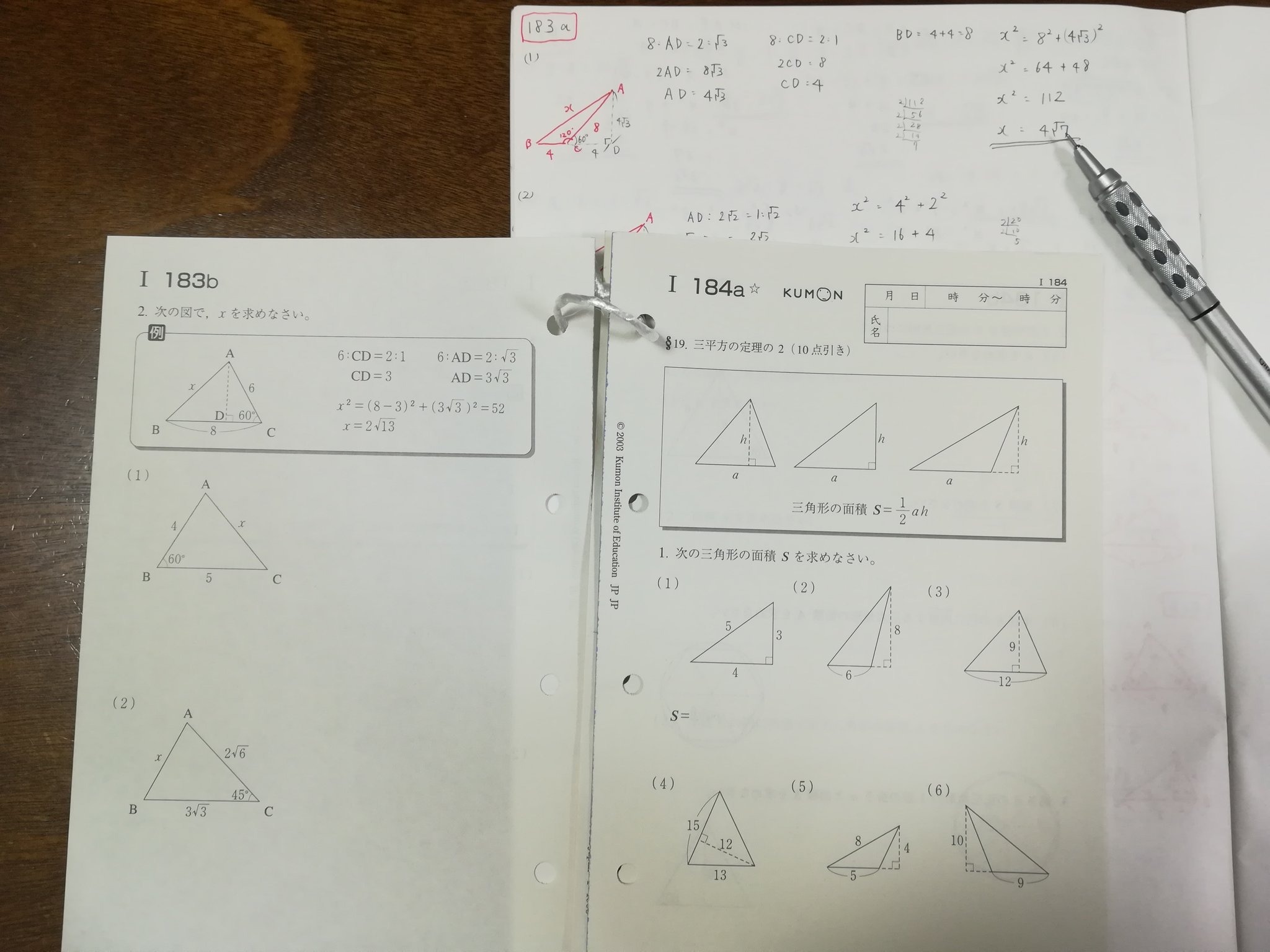
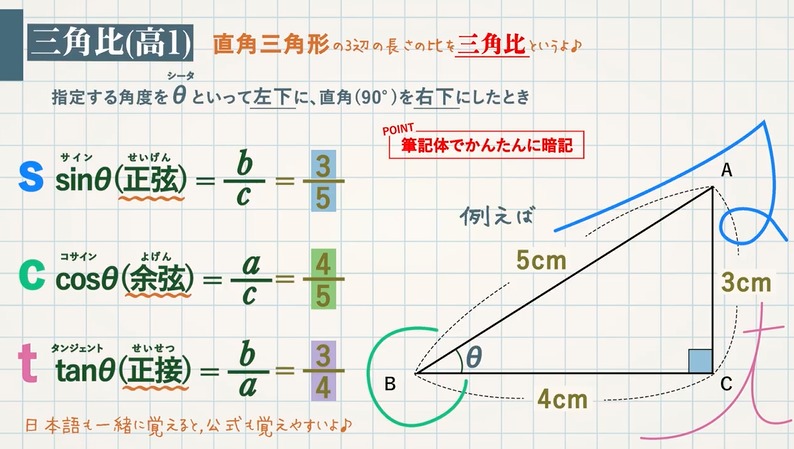
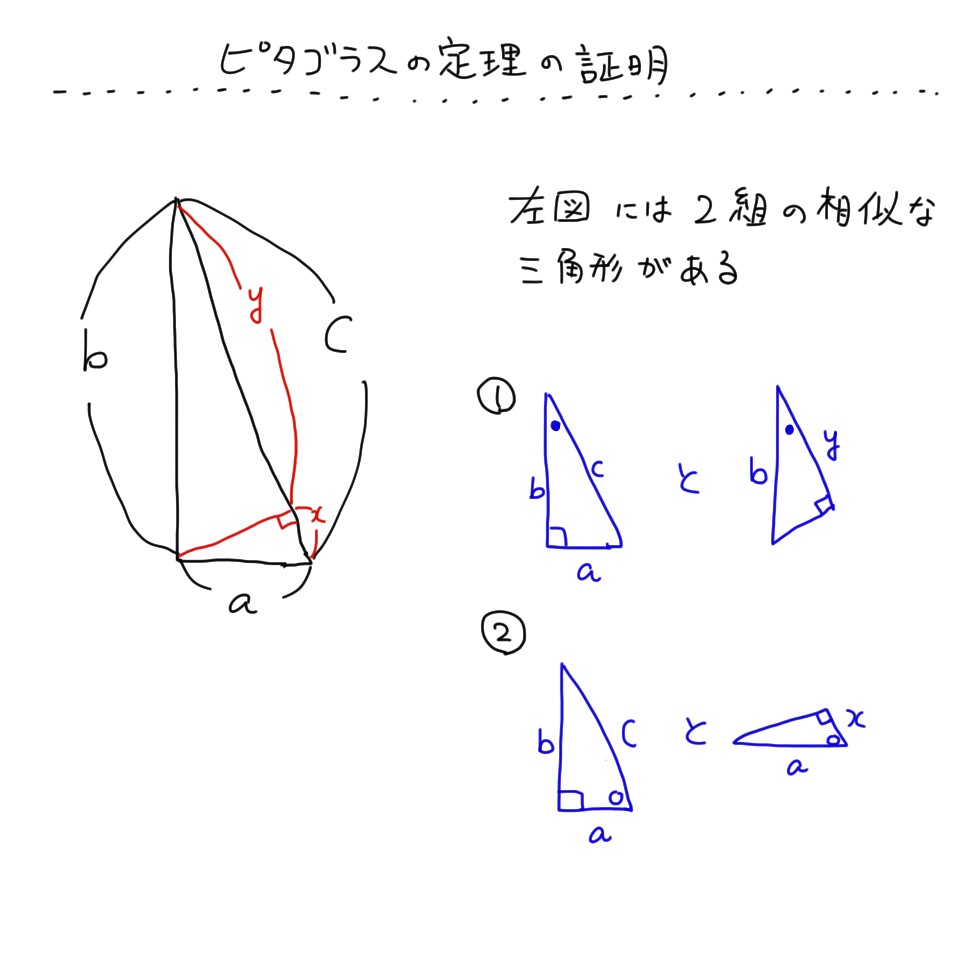
おさらいとして三平方の定理は以下の通り。 これに対して、逆も成り立ちます。 三角形の各辺に関して、 c2 = a2 b2 c 2 = a 2 b 2 という関係にあるなら、その三角形は直角三角形であるといえます。 そして、以下の2種類の直角三角形を覚える必要があります。 これらの角の大きさと辺の比をしっかり対応させましょう。 それぞれの辺の比は二等辺三角形・正三角形の性質から導けますが、三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 a b 数学って必要? 今まで図形の話は、あまり役に立つものではないといってきましたが、この三平方の定理だけは違います。 単に三角形の斜辺の長さを求める定理にとどまりません。 これは、 何かの「長さを求める」ときの基本となる定理 ですし、 三角
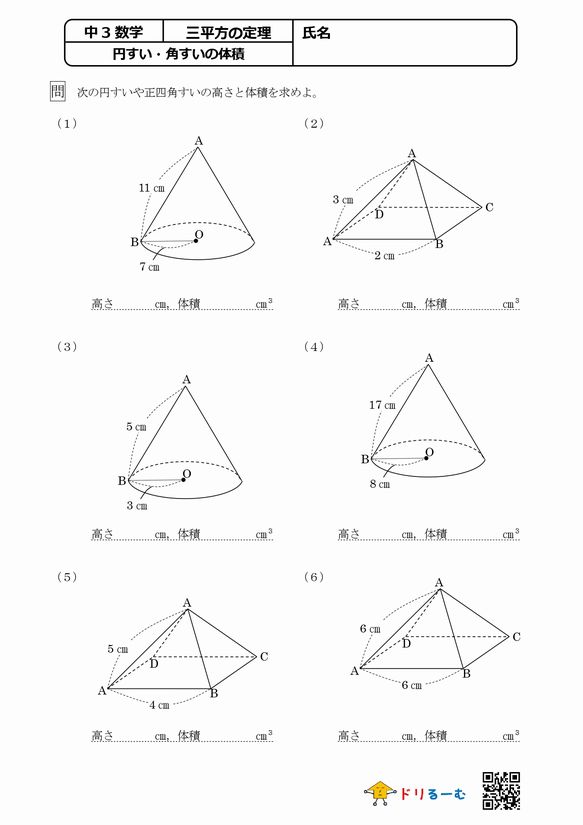
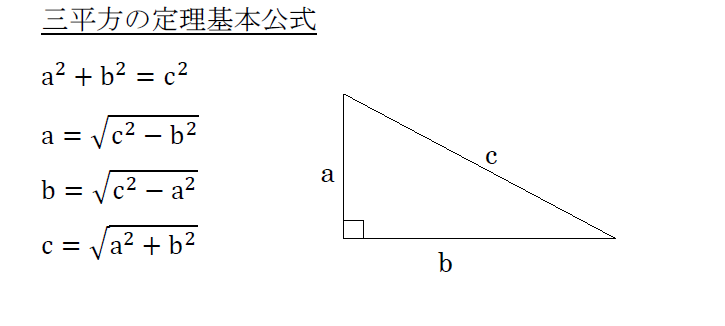
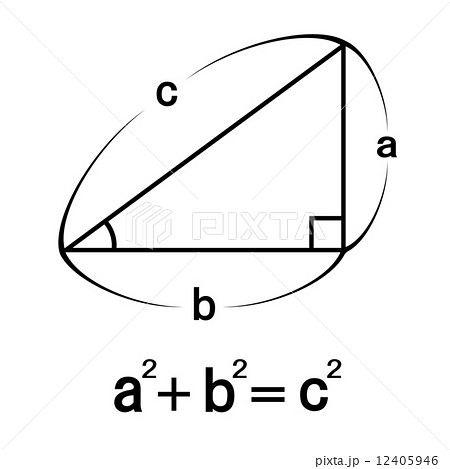
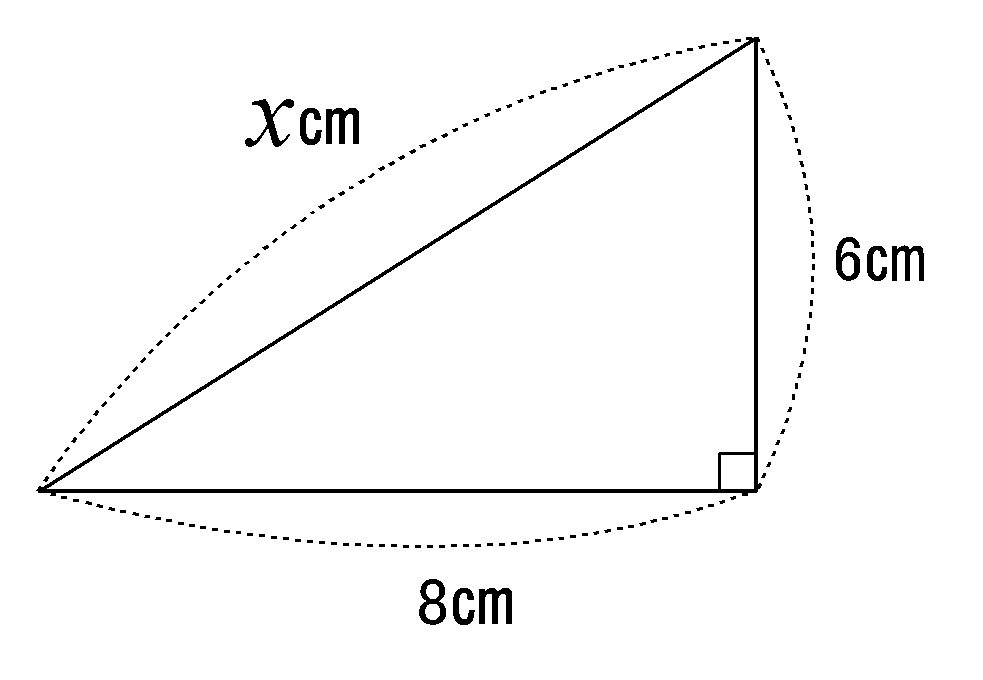
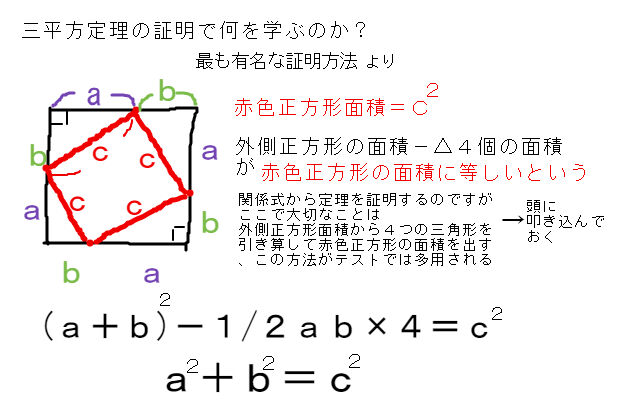
三平方の定理とは「直角三角形の辺の長さの関係」を示した定理であり、 直角をなす2辺を と 、2辺に対し斜めにとる残り1辺を とすると、 「 」 と表される。 やってみよう! 次の直角三角形の辺の長さを求めてみよう。 次の3辺をもつ三角形は直角三角形かどうか調べてみよう。 ,, ,, ,, こたえ 次の直角三角形の辺の長さを求めてみよう。 解説 三平方の定理に当てはめると、 となり、この値に平方重要 三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b とし、斜辺の長さを c とすると、次の関係が成り立つ。 c 2 = a 2 b 2 {\displaystyle c^ {2}=a^ {2}b^ {2}} この定理を証明したのは古代ギリシアの数学者ピタゴラスであるとも言われているので、この三平方の定理 (ピタゴラスの定理) c2= a2 b2 これだけです !!
数学 三平方の定理 難問のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  | |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
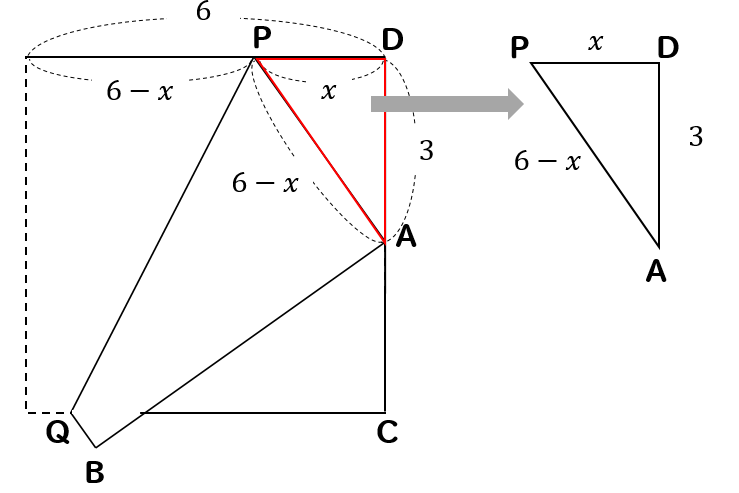
 |  | 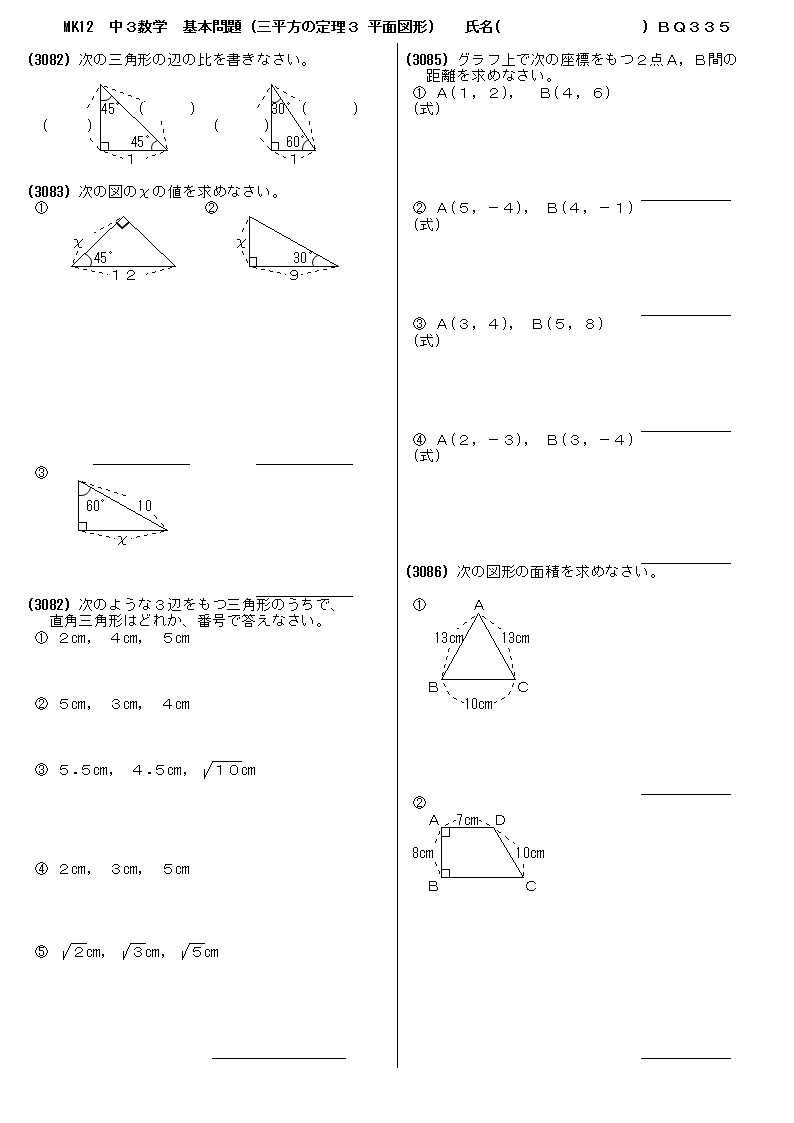 |
 |  |  |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 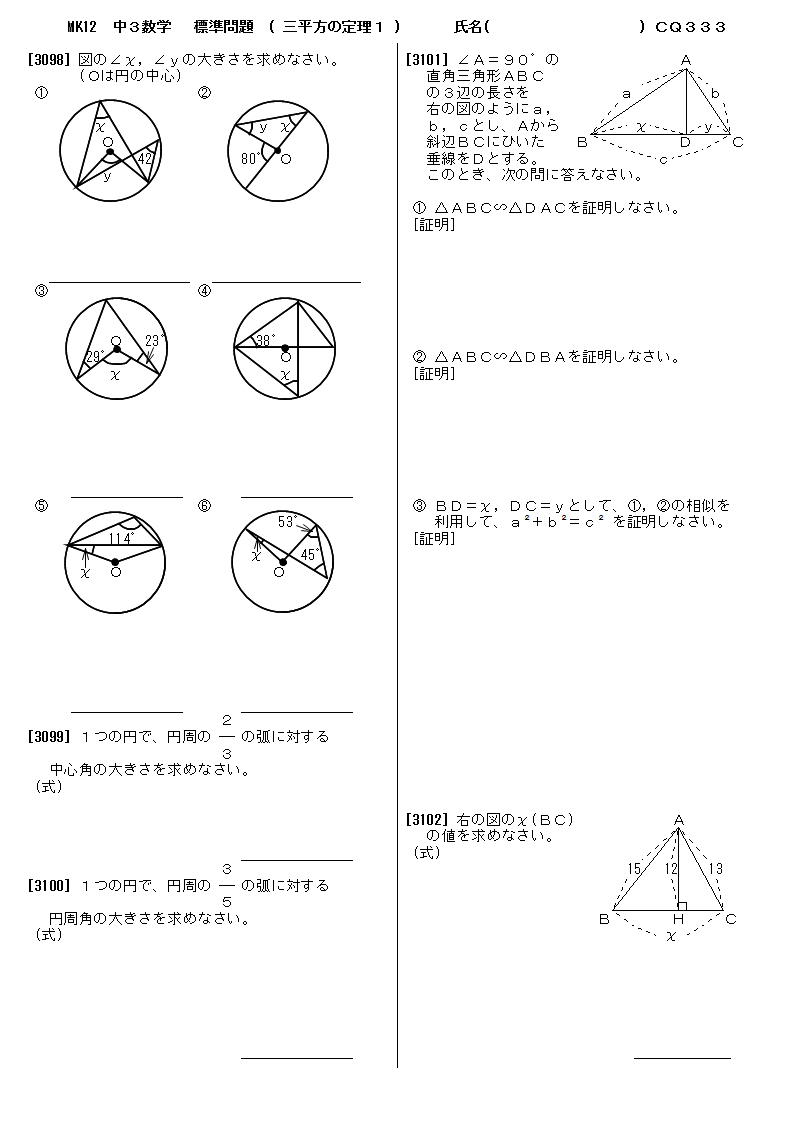 |
 |  |  |
 |  | |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | 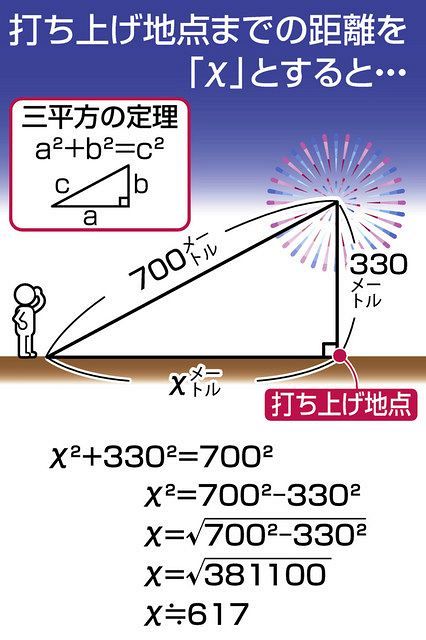 |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 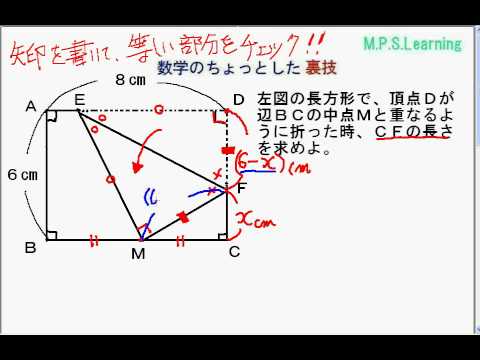 | 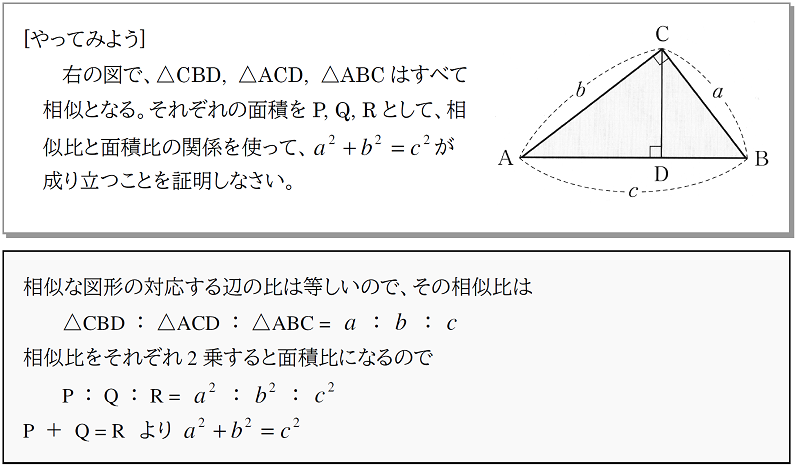 |
 | 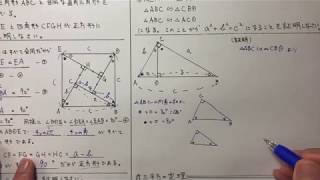 |  |
「数学 三平方の定理 難問」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
このような問題を解く場合には、三平方の定理の基本の式 $ a^2b^2=c^2 $ が成立するかを確認すればOKです。 ※cは一番長い辺 (斜辺) (1)の辺を $ a^2b^2=c^2 $ に当てはめると、 $ 12^25^2=13^2 $ $ =169 $ と式が背率するので、直角三角形であるといえます。 (2)の辺を $ a^2b^2=c^2 $ に当てはめると、 $ 4^25^2=7^2 $ $ 1625=49 $ こちらは左辺と右辺が 問題 問題三平方の定理・入試問題(高校入試)(中学3年生:第63回) 中学数学講座中3・三平方の定理動画講座一覧ページ 中学数学講座・動画一覧ページ ホーム 動画講座
Incoming Term: 数学 三平方の定理, 数学 三平方の定理 問題, 数学 三平方の定理 応用, 数学 三平方の定理 証明, 数学 三平方の定理 問題 応用, 数学 三平方の定理 難問, 数学 三平方の定理 立体, 数学 三平方の定理 ノート, 数学 三平方の定理 空間図形, 数学 三平方の定理とは,




0 件のコメント:
コメントを投稿